Statistical Learning Bias–variance Tradeoff

在知乎答：为什么样本方差的分母是n - 1？

翻译自之前的博客：Estimate Population Variance: should we divide by n - 1 or n

Posted by 贺鲲羽 on February 26, 2021

该回答写在知乎问题为什么样本方差（sample variance）的分母是 n-1？下，现搬运到此。内容与我的英文博客：Estimate Population Variance: should we divide by n - 1 or n 大致相同。

问题下已经有许多非常精彩的回答了。在估计总体方差时，比较常用的估计量（estimator）包括样本方差估计量 $s^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$和其最大似然估计量（maximum likelihood estimator, MLE）$\hat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$。

作为一个机器学习爱好者，我来从偏差-方差权衡（bias–variance tradeoff）的角度，结合Cochran定理比较一下二者的特性。先放上结论：

  1. 样本方差估计量的分母是 $n-1$的主要原因是我们希望获得一个总体方差的无偏估计量（unbiased estimator），这一点在许多回答中都已经被提及
  2. 总体方差的最大似然估计量有更低的方差（variance）和均方误差（mean square error，MSE），因而在一些场景中也适用

下文中，我们将首先回顾一下偏差-方差权衡，并介绍估计量的三个评价指标，偏差（bias）、方差、以及均方误差。

偏差-方差权衡

首先回顾一下偏差-方差权衡。当我们以估计量 $\hat{\theta}$估计总体参数 $\theta$时，估计偏误$\epsilon\left(\hat{\theta}\right)$可以表示为$\hat{\theta}-\theta$。作为衡量和比较估计量表现的评价指标，直观地讲，偏差衡量了估计值与总体参数的差距；而因为估计值是样本数据的函数，方差衡量了估计值在不同样本上与其平均值的离散程度。定义如下：

\begin{equation}\begin{aligned} \operatorname{MSE}(\hat{\theta})&:=\mathbb{E}[\epsilon^T \epsilon]=\mathbb{E}[\sum_{i=1}^p (\hat{\theta_i}-\theta_i)^2] \\ \operatorname{Bias}(\hat{\theta})&:=\left\Vert\mathbb{E}[\hat{\theta}]-\theta\right\Vert \\ \operatorname{Variance}(\hat{\theta})&:=\mathbb{E}\left[\left\Vert\hat{\theta}-\mathbb{E}[\hat{\theta}]\right\Vert_{2}^{2}\right] \end{aligned}\end{equation}

按照如下步骤，我们可以将均方误差分解为$(\text{bias}^2 + \text{variance})$：

\begin{equation}\begin{aligned} \text { Bias }^{2}+\text { variance } &=|\mathbb{E}[\hat{\theta}]-\theta|^{2}+\mathbb{E}\left[|\hat{\theta}-\mathbb{E}[\hat{\theta}]|^{2}\right] \\ &=\mathbb{E}[\widehat{\theta}]^{\top} \mathbb{E}[\hat{\theta}]-2 \theta^{\top} \mathbb{E}[\hat{\theta}]+\theta^{\top} \theta+\mathbb{E}\left[\hat{\theta}^{\top} \hat{\theta}-2 \widehat{\theta}^{\top} \mathbb{E}[\widehat{\theta}]+\mathbb{E}[\hat{\theta}]^{\top} \mathbb{E}[\widehat{\theta}]\right] \\ &=\mathbb{E}[\widehat{\theta}]^{\top} \mathbb{E}[\widehat{\theta}]-2 \theta^{\top} \mathbb{E}[\hat{\theta}]+\theta^{\top} \theta+\mathbb{E}\left[\widehat{\theta}^{\top} \hat{\theta}\right]-\mathbb{E}[\hat{\theta}]^{\top} \mathbb{E}[\widehat{\theta}] \\ &=-2 \theta^{\top} \mathbb{E}[\hat{\theta}]+\theta^{\top} \theta+\mathbb{E}\left[\hat{\theta}^{\top} \widehat{\theta}\right] \\ &=\mathbb{E}\left[-2 \theta^{\top} \hat{\theta}+\theta^{\top} \theta+\widehat{\theta}^{\top} \hat{\theta}\right] \\ &=\mathbb{E}[\left\Vert\theta-\hat{\theta}\right\Vert^{2}]=\operatorname{MSE}[\hat{\theta}] \end{aligned}\end{equation}

不难看出，均方误差是综合了偏差和方差的评价指标。

下面一节中，我们将运用Cochran定理分别计算样本估计量和总体方差的最大似然估计量的偏差、方差和均方误差并作比较。

评估样本方差估计量

Cochran定理的证明与回答的关系不大，此处略去。

其表明，一系列产生于标准正态分布且独立同分布（$\overset{iid}{\sim}N(0,1)$）的随机变量的平方和服从自由度为$(n-1)$ 的卡方分布（chi-square distribution）。

将结论用于分析样本方差估计量，不难看出$\frac{(n-1) s^{2}}{\sigma^{2}}=\sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{\sigma}\right)^{2} {\sim} \chi_{n-1}^{2}$。其中，$\frac{x_{i}-\bar{x}}{\sigma} \stackrel{iid}{\sim} N(0, 1) $。因此，$\mathbb{E}\left[\frac{(n-1) s^{2}}{\sigma^{2}}\right]=\mathbb{E}\left[\chi_{n-1}^{2}\right]=n-1$，即$\mathbb{E}\left[s^{2}\right]=\sigma^{2}$。也就是说：

\begin{equation}\begin{aligned}\operatorname{Bias}\left[s^{2}\right]&=\mathbb{E}\left[s^{2}\right]-\sigma^{2}=\sigma^{2}-\sigma^{2}\\&=0\end{aligned}\end{equation}

由此，样本方差估计量是总体方差的无偏估计量。

再看样本方差估计量的方差，$\operatorname{Var}\left(\frac{(n-1) s^{2}}{\sigma^{2}}\right)=\operatorname{Var}\left(\chi_{n-1}^{2}\right)=2(n-1)$。因此：

\begin{equation}\begin{aligned} \operatorname{Var}\left[s^{2}\right]&=\frac{2 \sigma^{4}}{n-1} \\ \operatorname{MSE}\left[s^{2}\right]&=\frac{2 \sigma^{4}}{n-1} \end{aligned}\end{equation}

类似地，将结论用于分析总体方差的最大似然估计量，不难看出$\mathbb{E}\left[\frac{n \hat{\sigma}^{2}}{\sigma^{2}}\right]=\mathbb{E}\left[\chi_{n-1}^{2}\right]=n-1$。因此：

\begin{equation}\begin{aligned}\operatorname{Bias}\left[\hat{\sigma}^{2}\right]&=\mathbb{E}\left[\hat{\sigma}^{2}\right]-\sigma^{2}=\frac{(n-1) \sigma^{2}}{n}-\sigma^{2}\\&=-\frac{1}{n} \sigma^{2}\le0 \end{aligned}\end{equation}

也就是说，总体方差的最大似然估计量是总体方差的有偏估计量，并且倾向于低估总体方差。再看其方差和均方误差。 $\operatorname{Var}\left(\frac{n \hat{\sigma}^{2}}{\sigma^{2}}\right)=\operatorname{Var}\left(\chi_{n-1}^{2}\right)=2(n-1)$，因此：

\begin{equation}\begin{aligned} \operatorname{Var}\left[\hat{\sigma}^{2}\right]&=\frac{2 \sigma^{4}(n-1)}{n^{2}} \\ \operatorname{MSE}\left[\hat{\sigma}^{2} \right]&=\left(-\frac{\sigma^{2}}{n}\right)^{2}+\frac{2 \sigma^{4}(n-1)}{n^{2}}\\&=\frac{\sigma^{4}(2 n-1)}{n^{2}} \end{aligned}\end{equation}

最后，我们以偏差、方差和均方误差作为评价标准，比较一下总体方差的样本方差估计量和最大似然估计量：

  • 如果以偏差作为评价标准：很直观地，样本方差估计量是总体方差的无偏估计量，总体方差的最大似然估计量会引入向下偏差，偏差的绝对值大小与总体方差参数成正比关系，与样本量成反比关系。样本方差估计量（分母为 $n-1$ ）更好。
  • 如果以方差作为评价标准：由$\operatorname{Var}\left[s^{2}\right]-\operatorname{Var} \left[\hat{\sigma}^{2}\right]=\frac{2 \sigma^{4}(2 n-1)}{n^{2}(n-1)}>0$可知最大似然估计量的方差更小，而且二者方差的差距与总体方差参数成正比关系，与样本量成反比关系。总体方差的最大似然估计量（分母为$n$）更好。
  • 如果以均方误差作为评价标准：由$\operatorname{MSE}\left[\hat{s}^{2} \right]- \operatorname{MSE}\left[\hat{\sigma}^{2} \right]=\frac{2 \sigma^{4}}{n(n-1)}>0$，可知最大似然估计量的均方误差更小，而且这一差距与总体方差参数成正比关系，与样本量成反比关系。总体方差的最大似然估计量更好。

下面一节，将以数值实验的形式验证上面三条结论。

数值实验

首先，按照 $\overset{iid}{\sim}N(0, \sigma^2)$生成一个样本量为100000，样本容量为 $n$的数据矩阵$X$ 。换句话说，$X$中的每一个列向量$X_{i, n\times 1}\overset{iid}{\sim}N(0, \sigma^2)$代表一个大小为$n$样本。我们可以尝试$n=10, \sigma^2=1$：

1
2
3
4
5
6
7
8
9
10
11
12

import numpy as np


np.random.seed(123)
LOC = 0
N = 100000

# Generate data
n = 10
sigma2 = 1

X = np.random.normal(LOC, sigma2, size=(n, N))

我们可以用下面的evaluate_var_estimator函数来计算总体方差的样本方差估计量和最大似然估计量的偏差，方差和均方误差：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def evaluateVarEstimator(X, ddof=1):
    est = X.var(axis=0, ddof=ddof)
    bias = est.mean() - sigma2
    var = est.var()

    return bias, var, bias ** 2 + var


to_print = ("{}: Bias = {:.4f}, Variance = {:.4f}"
            ", MSE = {:.4f}.")

print(to_print.format("Sample variance estimator", *evaluateVarEstimator(X)))
# Output: Sample variance estimator: Bias = 0.0001, Variance = 0.2225, MSE = 0.2225.

print(to_print.format("Sample variance estimator", *evaluateVarEstimator(X, ddof=0)))
# Output: MLE estimator: Bias = -0.0999, Variance = 0.1802, MSE = 0.1902.

与前面一节的结论相同地，样本方差估计量是总体方差的无偏估计量，而其最大似然估计量引入了向下偏差。与此同时，后者有更小的方差和均方误差。

下面，我们可以通过改变样本量$n$和总体方差参数 $\sigma^2$ 观察两个估计量偏差、方差和均方误差的差值的变化情况。使用如下代码简单验证：

1
2
3
4
5
6
7
8
9
10
11
12
13

ns = [10, 100, 1000]
sigma2s = [1, 10, 100]

gaps = np.zeros(shape=(3, len(ns), len(sigma2s)))

for i in range(len(ns)):
    for j in range(len(sigma2s)):
        X = np.random.normal(LOC, sigma2s[j], size=(ns[i], N))
        gap = np.array(evaluateVarEstimator(X)) -\
              np.array(evaluateVarEstimator(X, ddof=0))

        for l, metric in enumerate(gap):
            gaps[l, i, j] = metric

并且使用热力图（heatmap）可视化结果（每一个方格代表差值的大小）：

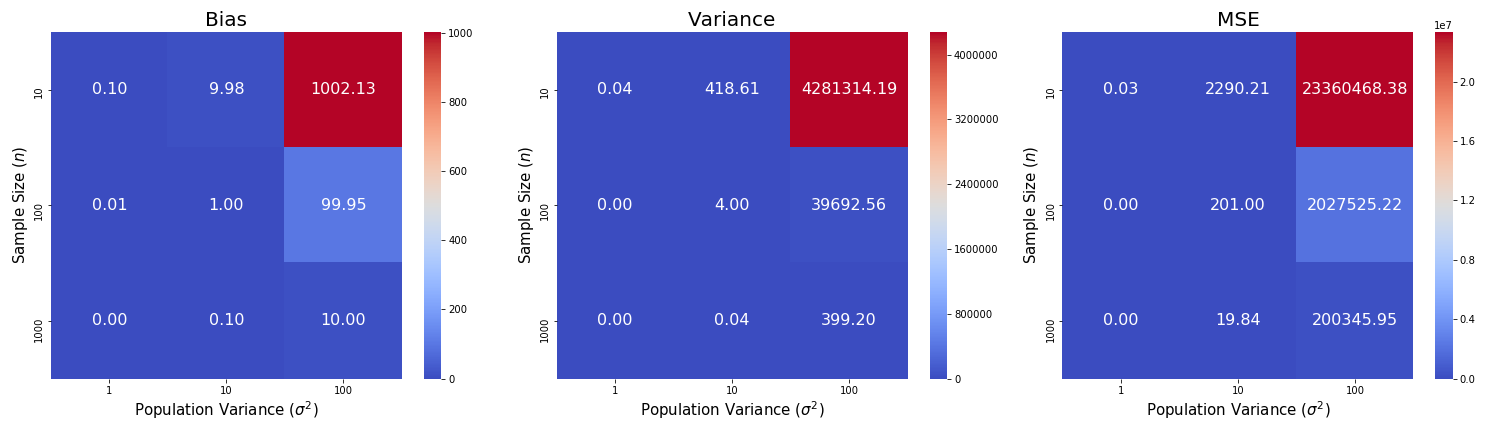
正如预期，偏差、方差和均方误差的差值随样本量$n$的增加而减小，随总体方差$\sigma^2$的增加而增加。

感谢阅读。最后，附上知乎回答链接：为什么样本方差（sample variance）的分母是 n-1？ - 知乎

Background picture source: valentin hintikka on Pixabay

CATALOG
    FEATURED TAGS
    Machine Learning SVD Bias–variance Tradeoff Linear Regression Statistical Learning
    FRIENDS